Primzahlen und ihre Bedeutung für das moderne Leben
Sie haben die Schule abgeschlossen oder sogar die Universität besucht? Wenn Sie sich für diesen Artikel interessieren, dann nehmen wir an, dass Sie zumindest die Grundlagen der Primzahlen verstehen. Primzahlen sind unglaublich und sie sind wesentlich, denn sie sind die Grundbausteine aller Zahlen. Darüber hinaus helfen sie uns, das Universum zu verstehen.
Wenn Außerirdische uns jemals eine Botschaft senden, dann wird dies durch Primzahlen geschehen, denn egal welches Jahrhundert, welcher Lebensstil oder welcher Trend gerade herrscht: Primzahlen ändern sich nie.
Sie wissen wahrscheinlich schon, was Primzahlen sind – wenn nicht, lesen Sie weiter. Primzahlen sind die Menge aller Zahlen, die nur durch eins und sich selbst geteilt werden können, wobei keine andere gerade Division möglich ist.
Zahlen wie 2, 3, 5, 7 und 11 sind Primzahlen, doch nur wenige wissen, wie bedeutend diese Zahlen sind und wie die mathematische Logik Primzahlen zu wichtigen Anwendungen in der modernen Welt nutzt.
Schauen wir uns etwas Faszinierendes über Primzahlen an. Mathematiker haben gezeigt:
Jede ganze Zahl kann als Produkt von Primzahlen, nur von Primzahlen und nichts anderem, ausgedrückt werden.
Zum Beispiel:
Um 222 zu erhalten, versuchen Sie 2 * 3 * 37
36230980? Das ist einfach 2 * 2 * 5 * 23 * 79 * 997
Oder sehen Sie sich in der folgenden Baumstruktur an, wie die oben genannten Primzahlen zusammengesetzt sind:
| 36230980 | ||||||
| / \ | ||||||
| 2 | 18115490 | |||||
| / \ | ||||||
| 2 | 9057745 | |||||
| / \ | ||||||
| 5 | 1811549 | |||||
| / \ | ||||||
| 23 | 78763 | |||||
| / \ | ||||||
| 79 | 997 |
Manchmal sieht die Berechnung anstelle von 2 * 2 * 5 * 23 * 79 * 997 wie folgt aus: 22 x 51 x 231 x 791 x 9971, was nur die Exponentialform desselben arithmetischen Prozesses ist.
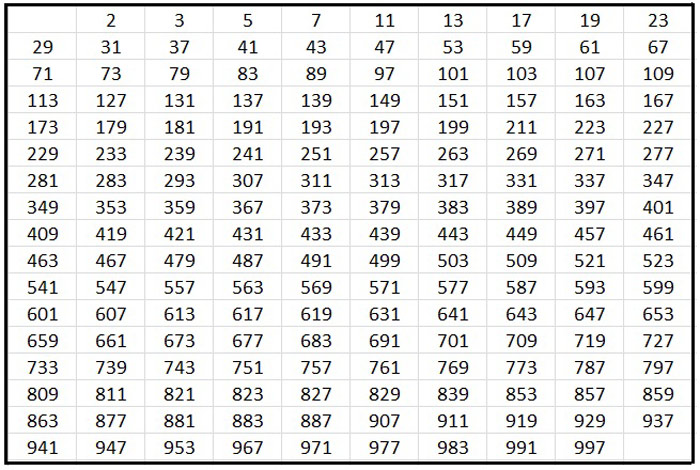
Führen Sie nun selbst einige einfache Berechnungen durch, um ein Gefühl dafür zu bekommen. Zu Ihrer Erleichterung haben wir eine Liste von Primzahlen beigefügt, die Sie ausprobieren können. Sie sehen folgend eine Tabelle mit allen Primzahlen bis zu 1000.
Diese grundlegende Regel wird als „Primfaktorzerlegung“ oder, wissenschaftlicher ausgedrückt, als „Fundamentalsatz der Arithmetik“ [1] bezeichnet.
Man kann eine Primzahl nicht weiter zerlegen. Wenn wir also versuchen, eine beliebige Zahl in zwei Zahlen zu teilen, diese wiederum, wenn möglich, in zwei weitere Zahlen teilen und so weiter, werden wir schließlich nur noch Primzahlen vorfinden.
Manche mögen behaupten, dass dies nichts weiter als eine mathematische Kuriosität sei. Aber es gibt noch eine weitere Tatsache, die von Bedeutung ist, denn Mathematiker und Informatiker haben Folgendes festgestellt:
„Es ist unmöglich, eine effiziente Formel für die Zerlegung großer Zahlen in Primzahlen aufzustellen.“
Es gibt Möglichkeiten, große Zahlen in Primzahlen zu zerlegen. Wenn wir jedoch versuchen, eine 500-stellige Zahl mit demselben Algorithmus wie eine 7-stellige Zahl zu faktorisieren, würden die fortschrittlichsten Supercomputer der Welt [2] eine absurde Zeitspanne benötigen, um die Bausteine der Zahl – oder die Primzahlen – zu berechnen. Um Ihnen eine Vorstellung von der Größenordnung zu geben: Die Zerlegung einer 500-stelligen Zahl in ihre Primzahlen könnte so lange dauern, wie die Entstehung der Erde und bei größeren Zahlen könnte der Zerlegungsprozess länger dauern als das Alter des Universums selbst.
Wie wir feststellen können, ist die Größe der Zahlen, die wir in Primzahlen zerlegen können, in der Praxis begrenzt. Diese Tatsache ist für diemoderne Computersicherheit von entscheidender Bedeutung. Wenn wir nun das obige Problem aus der Perspektive der Computersicherheit betrachten, verstehen wir, dass ein großes Interesse daran besteht, das Problem zu lösen und dass die Fähigkeit, eine große Zahl in einer angemessenen Zeit in Primzahlen zu faktorisieren, eine Notwendigkeit ist.
Die meisten aktuellen Verschlüsselungsalgorithmen nutzen die Tatsache aus, dass wir zwei große Primzahlen einfach miteinander multiplizieren können, um eine neue, sehr große Zahl zu erhalten. Denn derzeit kann kein verfügbarer Computer diese supergroße Zahl schnell in die beiden zugrundeliegenden Primzahlen aufteilen.
Diese einfache mathematische Sicherheit ist die Grundlage für die so genannte Public-Key-Kryptographie[3], d.h. eine Verschlüsselungstechnik, bei der wir uns nicht um den öffentlichen Teil des Schlüssels kümmern müssen. Dieser öffentliche Schlüssel kann (und muss) offen an jeden Dritten verteilt werden, der den verschlüsselten Inhalt entschlüsseln möchte.
Die Kenntnis des öffentlichen Schlüssels zu verschlüsselten Informationen hilft Ihnen nicht, diese zu entschlüsseln. Bevor Sie die Datei oder Nachricht lesen können, müssen Sie die kritischen Faktoren des Verschlüsselungsschlüssels kennen. Und wie wir oben erklärt haben, können Sie das nicht selbst herausfinden.
Primzahlen und Cybersicherheit
Wie können Sie die ersten spezifischen Informationen, die für die Einrichtung einer sicheren Kommunikation erforderlich sind, auf sichere Weise übermitteln?
Bei der Kryptografie mit öffentlichen Schlüsseln, dem Rückgrat der Computerverschlüsselung, können wir dies umgehen, da die Einzelheiten der sicheren Kontaktaufnahme selbst nicht geschützt werden müssen.
Genau das Gegenteil ist der Fall – die Leute posten Links zu ihren öffentlichen Schlüsseln in den sozialen Medien, damit möglichst viele Leute in der Lage sind, Nachrichten für sie zu verschlüsseln. Obwohl es inzwischen eine ganze Reihe von Verschlüsselungsalgorithmen gibt, die sich die Primfaktorzerlegung zunutze machen, ist RSA[4] der historisch bedeutendste und immer noch das konzeptionelle Leitbild in diesem Gebiet.
Es gibt zwei Arten oft verwendeter Verschlüsselungssysteme: die symmetrische Verschlüsselung und die asymmetrische Verschlüsselung.
Die symmetrische Verschlüsselung ist sehr schnell, aber auch nicht ganz so sicher. Sie verwendet denselben Schlüssel für die Ver- und Entschlüsselung und wenn eine nicht vertrauenswürdige Person diesen Schlüssel findet, kann sie Ihre gesamten verschlüsselten Daten gefährden. Diese Art der Verschlüsselung kommt in der Regel bei Computer- oder Handytransaktionen zum Einsatz.
Vielleicht haben Sie schon bemerkt, dass Sie beim Online-Banking einen Sicherheitscode zugeschickt bekommen, bei dem es sich um einen symmetrischen Verschlüsselungscode handelt.
Abgesehen davon, dass er unsicher ist, muss sich der Schlüssel vor der Verwendung bei allen Mitgliedern einfinden. Hier kommt die Magie der asymmetrischen Verschlüsselung ins Spiel.
Bei asymmetrischer Verschlüsselung werden zwei Schlüssel anstelle eines Schlüssels verwendet. Einer ist für die Verschlüsselung zuständig, der andere für die Entschlüsselung. Dieser Ansatz funktioniert, weil ein Schlüssel öffentlich ist (Verschlüsselung) und der andere privat (Entschlüsselung). Daher kann nur derjenige, der über einen privaten Schlüssel verfügt, die Chiffre nach der Entschlüsselung auch verstehen. Dies schützt die Informationen vor Online-Hackern oder nicht vertrauenswürdigen Benutzern.
Diese Verschlüsselungsmethode funktioniert und bietet aufgrund ihrer Falltür-Funktionen ein hohes Maß an Sicherheit. Jeder, der einen öffentlichen Schlüssel hat, kann verschlüsseln, aber ein Zurückgehen zur Entschlüsselung ist nicht möglich.
Das Bild erleichtert das Verständnis der Falltür-Funktion. RSA, die am häufigsten verwendete Verschlüsselung, verwendet ebenfalls ein asymmetrisches Verschlüsselungsverfahren.
RSA ist ein Verschlüsselungssystem, dessen Entwicklung auf der Grundlage einfacher Zahlenoperationen beruht. Dieses System sichert Informationen online – es ist eine bevorzugte Methode, weil die in Primzahlen zerlegten Zahlen multipliziert werden.
„Wenn zum Beispiel 11 und 17 multipliziert werden, um die Zahl 187 zu erhalten, ergibt die Aufschlüsselung die gleichen zwei Ausgangszahlen. Je größer also die Zahl ist, desto stärker ist die Verschlüsselung.“
Wir verwenden die Computerverschlüsselung ständig, z.B. wenn wir unsere Kreditkartendaten an einen Online-Händler übermitteln, uns bei unserer Bank anmelden oder eine manuell verschlüsselte E-Mail an einen Kollegen senden. Zusammengefasst bedeutet dies, dass wir uns in unserem gesamten virtuellen Leben auf Primzahlen tagein, tagaus verlassen.
Primzahlen zu verstehen ist weder eine sinnlose Suche noch eine rein wissenschaftliche Herausforderung. Vielmehr geht es darum, die Grenzen unserer Sicherheit besser zu verstehen, vor allem wenn man bedenkt, dass es bei der Faktorisierung großer Zahlen schon seit Jahren keine Fortschritte mehr gibt.
Forscher haben hunderte Computer miteinander vernetzt, um das Äquivalent an Leistung zu generieren, für die ein einzelner Computer mehrere tausend Jahre benötigen würde. Dabei wurden fortschrittliche Faktorisierungsalgorithmen verwendet, um die „RSA-768“-Zahl zu faktorisieren, d.h. eine Zahl mit 232 Ziffern, die von der RSA-Gruppe als Faktorisierungsaufgabe gestellt wurde.
Der Nachweis, dass es möglich war, die 768-Bit-Verschlüsselung in einer Zeit zu entschlüsseln, die unter der Zeitspanne vom Anbeginn bis zumWärmetoddes Universums liegt, ist für die Welt der Sicherheitsexperten inakzeptabel. Als Reaktion darauf wurde der Standard für moderne Verschlüsselung auf RSA-1024 mit 309 Ziffern und RSA-2048 mit 617 Dezimalziffernumgestellt.
Primzahlen in der Quanteninformatik
1024- und 2048-Bit-Verschlüsselungen sollen, soweit wir wissen, vor jedem sicher sein, der nicht im Besitz einer Zeitmaschine ist. In jüngster Zeit wird jedoch in Romanen wie Digital Fortress von Dan Brown [5] und Contact von Carl Sagan [6] auf ein geheimes NSA-Projekt verwiesen, das vermutlich über eine geheime Quantencomputertechnologie[7] verfügt, die selbst 2048-Bit-Verschlüsselungen in angemessener Zeit entschlüsseln kann.
Quantencomputing ist in letzter Zeit stark in der Presse vertreten und Google und die NASA arbeiten an einem Projekt, um es zu einem neuen Standard zu erheben. Es gibt jedoch keinen Beweis dafür, dass man mit Quantencomputing Zahlen entschlüsseln kann, die auf einer 1024- oder 2048-Bit-Verschlüsselung basieren.
Der Quantencomputer-Algorithmus wurde 1994 von Peter Shor entdeckt. Sein Algorithmus eignet sich hervorragend für die ganzzahlige Faktorisierung, d. h. man gibt eine ganze Zahl ein, und er berechnet deren Primzahlen.
Dieser Algorithmus war bei der Entschlüsselung recht erfolgreich und kann auch kleinere Primzahlen faktorisieren. Allerdings ist er noch nicht in der Lage, das RSA-Verfahren zu entschlüsseln. Die Forschung ist noch nicht abgeschlossen – an dem Tag, an dem der Algorithmus das RSA-Verfahren entschlüsseln kann, werden alle Konzepte des Online-Datenschutzes in sich zusammenfallen.
Die Entschlüsselung von Primzahlen ist eine Millionen-Dollar-Frage. Wirklich! Das Clay Mathematics Institute in Cambridge hat einen Millionenpreis für denjenigen ausgelobt, der einen Beweis für die Riemann-Hypothese erbringen kann.
Sie fragen sich vielleicht, wie die Riemann-Hypothese mit dem Quantencomputing zusammenhängt. Nun, die Verbindung zwischen den beiden ermöglicht eine neue Methode des Quantencomputings, die möglicherweise Primzahlen entschlüsseln kann.
Die Anwendung der Riemannschen Hypothese würde bedeuten, dass Primzahlen vorhersehbar geteilt werden, analog zu den Nullen in der Riemann-Zeta-Funktion. Der Beweis dafür würde auch die Millionen-Dollar-Frage lösen.
Viele Mathematiker sind der Meinung, dass die einzige exakte Entschlüsselungsmethode durch Quantencomputing erfolgen wird. Derzeit liegt der Schwerpunkt auf experimentellen Implementierungen des Quantencomputings.
Von besonderer Bedeutung ist die Primzahlfaktorisierung als Grundbaustein aller Zahlen, die die Wurzel für das Verständnis des Universums bilden [8].
Manche Mathematiker beschreiben die Zahlentheorie ein wenig wie Archäologie. Man hat nicht das Gefühl, moderne Technologien zu erfinden, sondern die logischen Grundlagen des Universums aufzudecken, die sein Verhalten überall und zu jeder Zeit beschreiben.
Das CodeCoda Research Lab arbeitet, inspiriert von Digital Fortress, an einem Konzept für einen neuen Verschlüsselungsalgorithmus, der es unmöglich macht, ihn durch Faktorisierung von Zahlen zu entschlüsseln. Daher ist der „Fundamentalsatz der Arithmetik“ einer der Bausteine für einen solchen Algorithmus. Ein detailliertes Verständnis der Primzahlen ist für die Entwicklung der nächsten Generation quantensicherer Verschlüsselungen unerlässlich.
Trotz dieser Aufregung würde die Möglichkeit der Entschlüsselung nicht das Ende der Sicherheit bedeuten. Auch wenn das Quantencomputing in der Lage sein wird, Chiffren zu entschlüsseln, so gibt es doch bereits zahlreiche Sicherheitstechnologien, die bereits im Vorfeld entwickelt und eingesetzt wurden.
Die Bedeutung von Primzahlen für das moderne Leben
Wir können Primzahlen auf verschiedenen Ebenen in unser Leben integrieren. Zum Beispiel verwenden wir Primzahlen für die Übermittlung unserer Kreditkarteninformationen an Online-Shops. Ein äußerst wichtiger Aspekt, den man über Primzahlen wissen muss, ist, dass sie außergewöhnliche Eigenschaften bei der Faktorisierung aufweisen. Eine davon ist, dass es elementar ist, größere Primzahlen zu finden. Allerdings sind diese schwieriger zu faktorisieren.
Primzahlen sind für die Kommunikation unverzichtbar, und ein Großteil der Computerkryptografie arbeitet mit ihnen. Nicht nur das, auch die Verschlüsselung von Dateien funktioniert über Primzahlen. Ob es sich um die Übermittlung von Rechnungsdaten, die Anmeldung bei einem Konto oder sogar um den Versand von E-Mails handelt, all dies geschieht durch Verschlüsselung.
Die Verschlüsselung oder Sicherheit, die unsere persönlichen Daten vor dem Zugriff durch Dritte schützt, ist auch das Werk der Primzahlen. Diese Eigenschaft zeigt, dass Primzahlen in der modernen, technologiebezogenen Lebensweise von wesentlicher Bedeutung sind. Daher ist jede Einschränkung im Bereich der Primzahlen eine Einschränkung, die wir alle erleben und spüren werden.
Die Entschlüsselung erfolgt durch die Faktorisierung höherwertiger Primzahlen. Diese Faktorisierung ist jedoch nur zur vorübergehenden Verwendung gedacht. Eine tatsächliche Faktorisierung von Primzahlen ist selbst für einen Supercomputer unmöglich. Dennoch besteht die Hoffnung, dass Quantencomputer in Zukunft in der Lage sein werden, dieses Problem zu lösen.
Primzahlen sind auch auf unseren Computerbildschirmen zu finden – sie verstärken die Farbe der Pixel. Sie werden von den Herstellern auch verwendet, um Oberschwingungen in Produkten zu beseitigen. Darüber hinaus bilden sie die Grundlage für die Computersicherheit, die im Zeitalter des einfachen Informationsaustauschs unerlässlich ist.
Viele Theoretiker messen Primzahlen große Bedeutung bei, weil sie Grundlage der ganzen Zahlen sind. Sie sind jedoch auch Zahlen mit ungewöhnlichen mathematischen Eigenschaften und finden in der heutigen technologischen Ära breite Anwendung.
Die Rolle der Primzahlen ist auch außerhalb unserer sorgfältig konstruierten Welt sichtbar – in der Natur. Wissenschaftliche Untersuchungen zeigen zum Beispiel, dass Zikaden Primzahlen verwenden, um ihre Eier abzulegen und ihre Höhlen zu verlassen. Sie verlassen ihre Höhlen in Intervallen von 7, 13 oder 17. Die Wissenschaftler vermuten, dass sie Primzahlen verwenden, um zu verhindern, dass sich Raubtiere annähern und sie fressen. Mit anderen Worten: Diese Insekten sind auf Primzahlen angewiesen, um zu überleben.
Primzahlen sind in der Volkskultur weit verbreitet. Viele Sänger, Schriftsteller und Künstler haben sich von ihnen inspirieren lassen. Carl Sagan zum Beispiel schrieb ein Buch über die Kommunikation mit Außerirdischen durch Primzahlen. Diese positiven Darstellungen und Erkenntnisse inspirieren auch Menschen, die nicht im wissenschaftlichen oder mathematischen Bereich arbeiten.
Sogar das populäre Spiel Candy Crush verwendet wissenschaftliche Theorien und mathematische Prinzipien, von denen die meisten ohne die Primzahlen nicht existieren würden. So hätte beispielsweise die Zahlentheorie ohne Primzahlen nie das Licht der Welt erblickt.
Wie auch immer man zu diesen einzigartigen Zahlen stehen mag, es lässt sich nicht leugnen, dass sie ein grundlegender Aspekt des Universums sind. Die laufende Forschung wird uns bei der Entwicklung der Primzahlen helfen.
Primzahlen haben ein immenses Potenzial, das in vielen bemerkenswerten Projekten intensiv genutzt wird. Außerdem können wir durch intensives Studium der Primzahlen viel über die Welt und zahlreiche technische Errungenschaften lernen.
Quellen
- Grundlegender Lehrsatz der Arithmetik
- Supercomputer
- RSA Beschreibung auf Wikipedia
- Kryptographie mit öffentlichem Schlüssel auf Wikipedia
- Digital Fortress, Dan Brown, 1998
- Contact, Carl Sagan, 1985
- Die Bits, die Bytes und die Quanten, Andreas Maier
- Warum Mathematik die Sprache des Universums ist, Team Futurism, 2013

